「StreamCipher」线性反馈移位寄存器

什么是线性反馈移位寄存器

我先递归学习了几个数学概念

母函数（生成函数）

普通型母函数

定义:

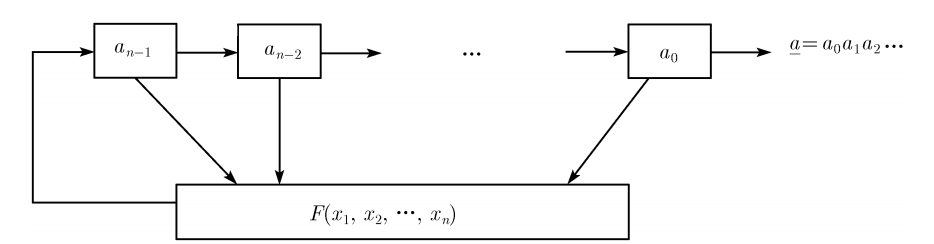
对于任意一个数列 $a_0,a_1,a_2\cdots a_n$, 用它的每一项可以定义一个函数:

$$ G(x)=a_0+a_1x+a_2x^2+\cdots +a_nx^n $$

则G(x)是数列的生成函数, 或者更准确地说, 是一个无穷级数

虽然说是一个无穷级数, 但我们可以设置$j>n$时, $a_j=0$之类的, 使得G(x)成为一个n次多项式, 但又是一个无穷序列 (doge

更数学一点的表示形式如下:

$$ G(a_n;x)=\Sigma_{n=0}^\infty a_nx^n $$

指数型母函数

一般形式为:

$$ EG(a_n;x)=\Sigma_{n=0}^\infty a_n\frac{x^n}{n!} $$

有限数域上的LFSR

说明与定义

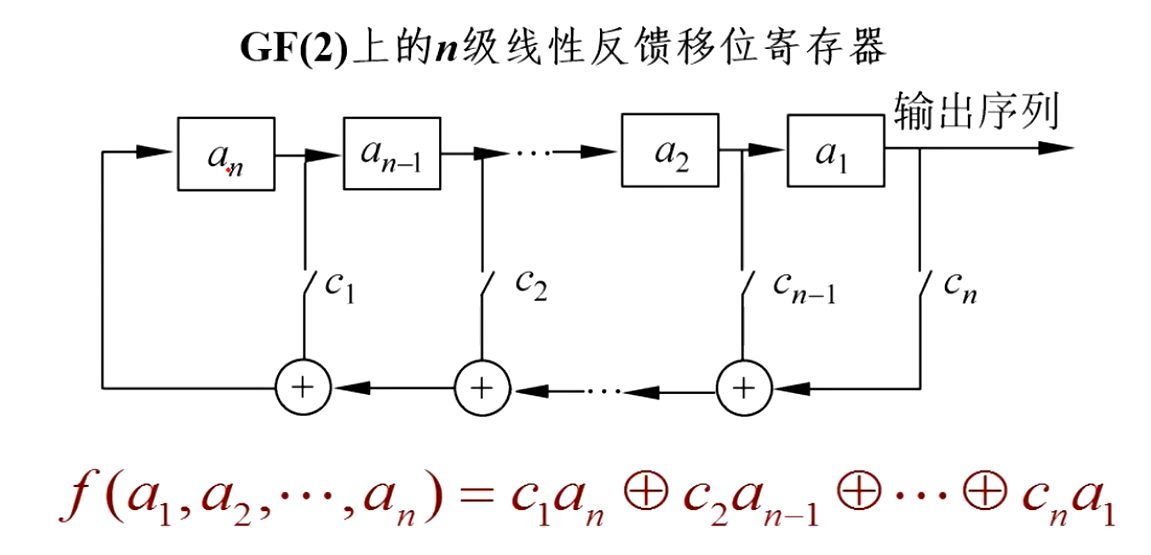
• 移位寄存器主要功能是产生密钥流
• gf(2) 表示存储器为二元存储器, 只能取 0 或 1
• n 级表示 n 个存储器
• 线性表示反馈函数 $f(a1, a2, …, an)$ 为线性函数, 运算有与或非, 与反馈移位寄存器的状态有关, 状态有 $2^n$ 种
• 初始状态由用户决定

可作递推模拟如下:

$$ a_{n+t}=c_1a_{n+t-1}\bigoplus c_2a_{n+t-2}\bigoplus\cdots \bigoplus c_na_{t}, t=1,2,\cdot \cdot \cdot $$

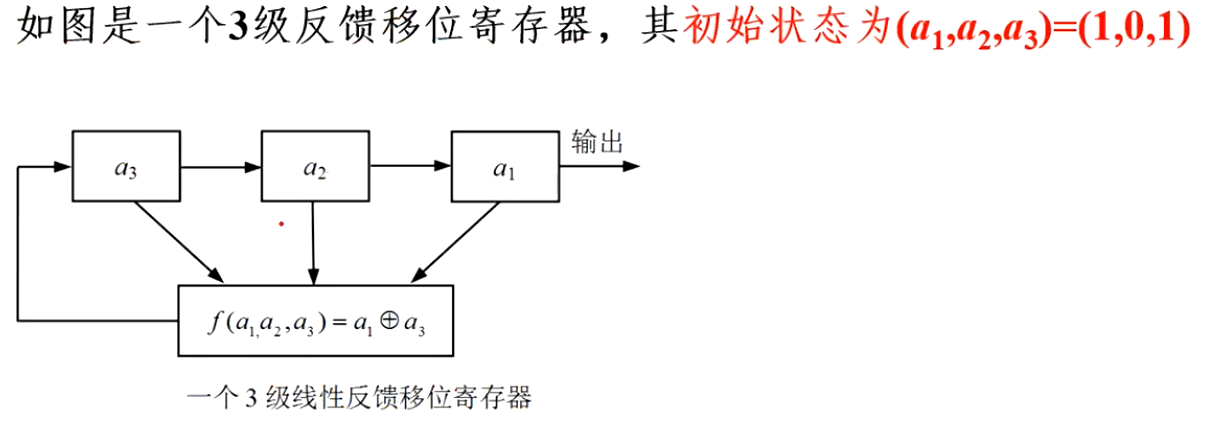
让我们看一个 3 级的例子:

定义初始状态为

则$a_4=a_1\bigoplus a_3=0$, 然后流出一个 $a_1$, 3 个寄存器变为

反馈函数变为 $f(a_2,a_3,a_4)=a_2\bigoplus a_4$

反复进行几轮上述操作, 就可以得到输出序列, 以及周期

LFSR 输出序列的性质

线性反馈移位寄存器实现起来简单, 速度快, 而且有较为成功的理论, 成为构造密钥流生成器的最重要的部件之一.

我们总是假定 $c_1,c_2,…,c_n$ 中至少有一个不为0, 否则$f(a1,a2,…,an)=0$, 总是假定 $c_n = 1$.

• $n级LFSR状态数：最多有2^n个$
• $n级LFSR的状态周期：\leq2^n-1$
• $输出序列的周期=状态周期\leq2^n-1$
• 选择合适的反馈函数可使序列的周期达到最大值 $2^n-1$, 周期达到最大值的序列称为 m 序列

数学推导与算法

摘自CTFwiki

线性反馈移位寄存器的反馈函数一般如下:

$$ a_{i+n} = \Sigma_{j=1}^n c_ja_{i+n-j} \tag{1} $$

其中, $c_j$均在某个有限域 $F_q$ 中.

进而, 可以求得其特征多项式为:

$$ f(x)=x^n-\Sigma_{i=1}^n c_ix^{n-i} \tag{2} $$

通过线性变换:

$$ \begin{bmatrix} a_{i+1},\ a_{i+2},\ a_{i+3},\cdots,\ a_{i+n} \end{bmatrix} \\ = \begin{bmatrix} a_{i+1},\ a_{i+2},\ a_{i+3},\cdots,\ a_{i+n} \end{bmatrix} \begin{bmatrix} 0 & 0 & \cdots & 0 & c_n \\ 1 & 0 & \cdots & 0 & c_{n-1} \\ 0 & 1 & \cdots & 0 & c_{n-2} \\ \vdots& \vdots &\ddots&\vdots \\ 0 & 0 & \cdots & 1 & c_1 \end{bmatrix} \\ = \begin{bmatrix} a_{0},\ a_{1},\ a_{2},\cdots,\ a_{n-1} \end{bmatrix} \begin{bmatrix} 0 & 0 & \cdots & 0 & c_n \\ 1 & 0 & \cdots & 0 & c_{n-1} \\ 0 & 1 & \cdots & 0 & c_{n-2} \\ \vdots& \vdots &\ddots&\vdots \\ 0 & 0 & \cdots & 1 & c_1 \end{bmatrix} ^{i+1} $$

同时, 定义其互反多项式为:

$$ \bar f(x) = x^nf(\frac 1 x) = 1 - \Sigma_{i=1}^n c_ix^i $$

也称互反多项式为线性反馈移位寄存器的联结多项式.

特征多项式与生成函数

已知某个 n 级线性反馈移位寄存器的特征多项式, 那么该序列对应的生成函数为:

$$ A(x) = \frac {p(x)} {\bar f(x)} $$

其中 $p(x) = \Sigma_{i=1}^n(c_{n-i}x^{n-i}\Sigma_{j=1}^ia_jx^{j-1})$. 可以看出 $p(x) $完全由初始状态和反馈函数的系数决定.

序列周期与生成函数

序列的的周期为其生成函数的既约真分式的分母的周期.

对于 n 级线性反馈移位寄存器, 最长周期为 $2^n−1$ (排除全零). 达到最长周期的序列一般称为 m 序列.

特殊性质

• 将两个序列累加得到新的序列的周期为这两个序列的周期的和
• 序列是 n 级 m 序列, 当且仅当序列的极小多项式是 n 次本原多项式

B-M 算法

一般来说, 我们可以从两种角度来考虑 LFSR

• 密钥生成角度, 一般我们希望使用级数尽可能低的 LFSR 来生成周期大, 随机性好的序列
• 密码分析角度, 给定一个长度为 n 的序列 a, 如何构造一个级数尽可能小的 LFSR 来生成它. 其实这就是 B-M 算法的来源

一般来说, 我们定义一个序列的线性复杂度如下

• 若 s 为一个全零序列, 则线性复杂度为 0
• 若没有 LFSR 能生成 s, 则线性复杂度为无穷
• 否则 s 的线性复杂度为生成 L(s) 的最小级的 LFSR

BM 算法的要求我们需要知道长度为 2n 的序列. 其复杂度

• 时间复杂度：$O(n^2)$ 次比特操作
• 空间复杂度：$O(n) $比特

关于 BM 算法的细节, 后续添加, 目前处于学习过程中.

但是其实如果我们知道了长度为 2n 的序列, 我们也可以一种比较笨的方法来获取原先的序列. 不妨假设已知的序列为 $a_1,…,a_{2n}$, 我们可以令:

$$ S_1=(a_1,…,a_n) \\ S_2=(a_2,…,a_{n+1}) \\ \cdots \\ S_{n+1}=(a_{n+1},…,a_{2n}) $$

那么我们可以构造矩阵 $X=(S_1,…,S_n)$, 那么

$S_{n+1}=(c_n,…,c_1)X$

所以 $(c_n,…,c_1)=S_{n+1}X^{−1}$

进而我们也就知道了 LFSR 的反馈表达式, 进而我们就可以推出初始化种子.

例子

2018 CISCN 初赛 oldstreamgame

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

flag = "flag{xxxxxxxxxxxxxxxx}"
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==14

def lfsr(R,mask):
    output = (R << 1) & 0xffffffff # R<<1, 取低32位, 最后一位是0
    i=(R&mask)&0xffffffff # R和mask与一下
    lastbit=0
    while i!=0:
        lastbit^=(i&1) # i由最后一位逐位向最高位异或, 存在lastbit中, lastbit只有1个bit
        i=i>>1
    output^=lastbit # out的最后一位变成lastbit, 其它不变
    return (output,lastbit)

R=int(flag[5:-1],16) # 长度为8*4=32bits, 内容为16进制
mask = 0b10100100000010000000100010010100 # 32bits

f=open("key","w")
for i in range(100):
    tmp=0
    for j in range(8):
        (R,out)=lfsr(R,mask)
        tmp=(tmp << 1)^out
    f.write(chr(tmp))
f.close()

下面细看一下mask的性质

• 只有第 3、5、8、12、20、27、30、32 位是 1, 其它都是 0, 这就导致如果 R 的对应位全不为 1, 那么 i 就为 0

• lastbit 是由 i 逐位向前异或的, 碰到 0 可以忽略, 所以 lastbit 最后的值取决于 i 中 1 的个数, 如果是奇数个 1, 则 lastbit 为 1；否则 lastbit 为 0. 而 i 中 1 的奇偶数取决于 R 的 3、5、8、12、20、27、30、32位

• 于是可以得到线性反馈函数

  $$ lastbit=R_3\bigoplus R_3\bigoplus R_5\bigoplus R_8\bigoplus R_{12}\bigoplus R_{20}\bigoplus R_{27}\bigoplus R_{30}\bigoplus R_{32} $$

下面开始求解

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

mask = '10100100000010000000100010010100'
key = '00100000111111011110111011111000'
tmp = key
R = ''
for i in range(32):
    output = '?'+key[:31]
    ans= int(tmp[-1-i])^int(output[-3])^int(output[-5])^int(output[-8])^int(output[-12])^int(output[-20])^int(output[-27])^int(output[-30])
    R += str(ans)
    key = str(ans) + key[:31]

R = hex(int(R[::-1], 2))[2::]
print('flag{'+R+'}')