♯
>> 文章 >> 标签 >> 分类 >> 友链 >> 我是
♯

「BUUOJ」NPUCTF2020 BabyObfuscation 静态分析

Tr4ccK  收录于  类别 TECHNOLOGY
     约 1362 字   预计阅读 3 分钟 
警告
本文最后更新于 2021-04-21，文中内容可能已过时。
  1. 发现是 64 位程序, 无壳
  2. 运行程序提示为 “WHERE IS MY KEY!?”

载入 IDA 后 main 函数:

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111

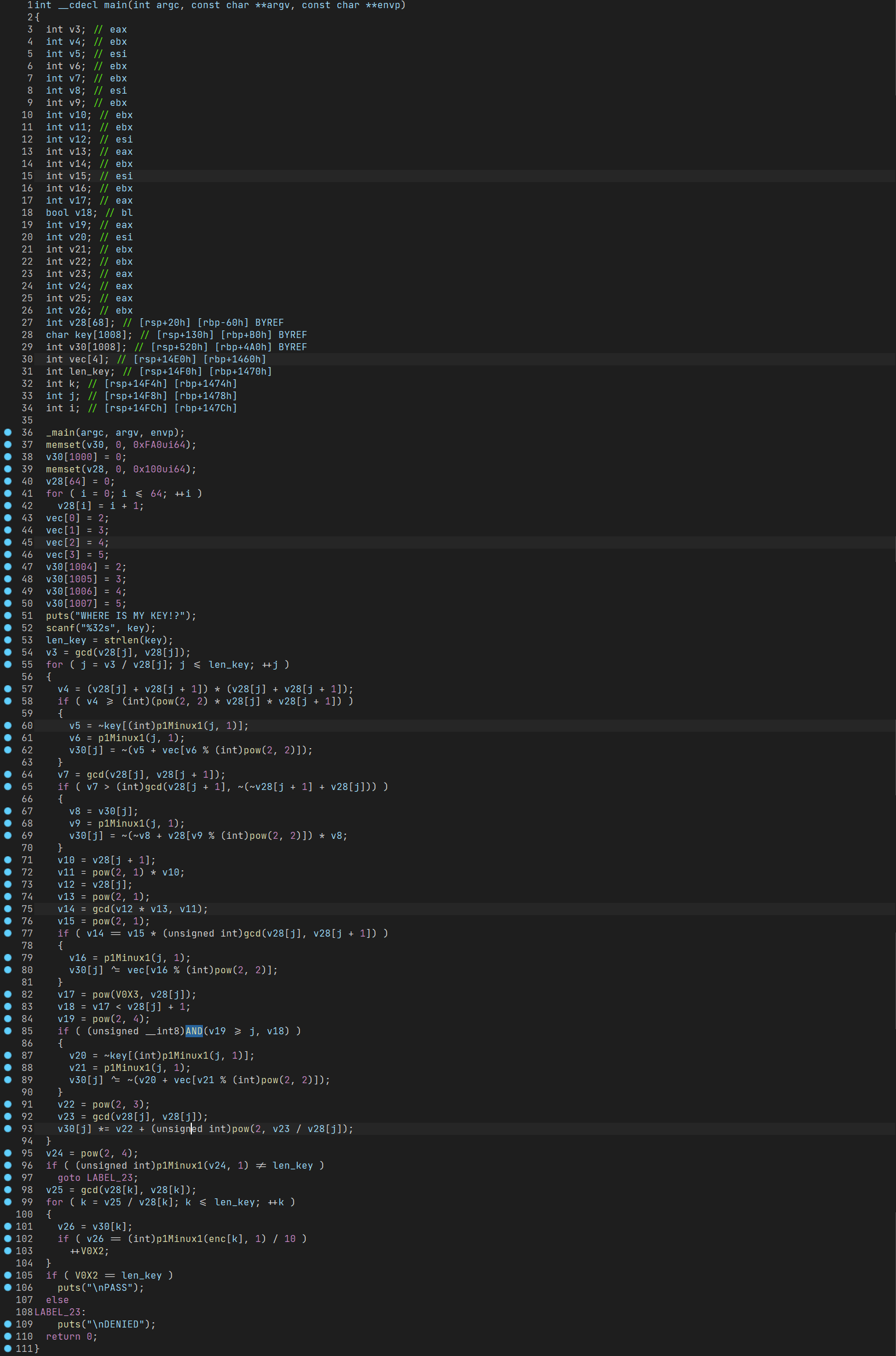
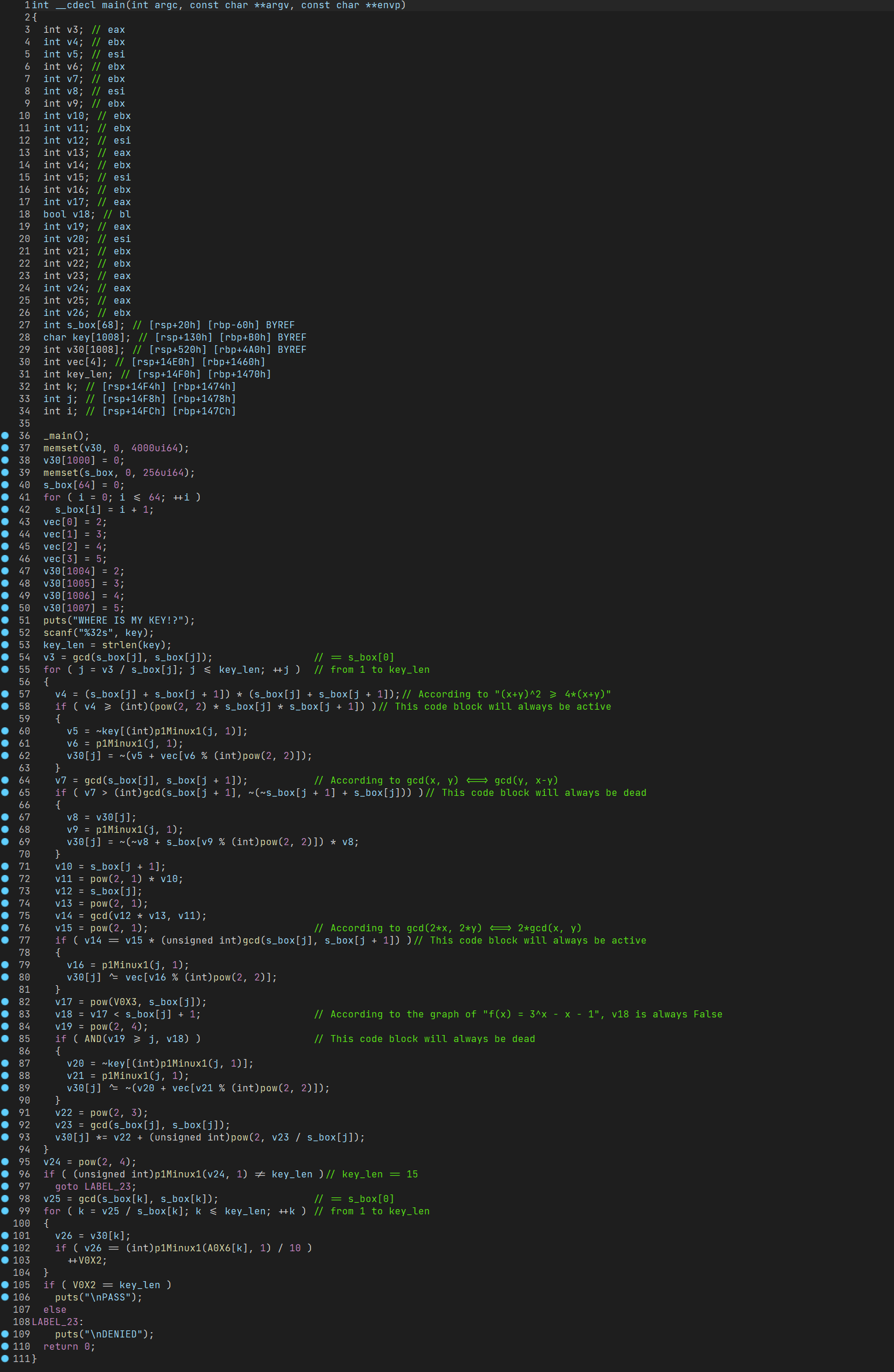
int __cdecl main(int argc, const char **argv, const char **envp)
{
  int v3; // eax
  int v4; // ebx
  int v5; // esi
  int v6; // ebx
  int v7; // ebx
  int v8; // esi
  int v9; // ebx
  int v10; // ebx
  int v11; // ebx
  int v12; // esi
  int v13; // eax
  int v14; // ebx
  int v15; // esi
  int v16; // ebx
  int v17; // eax
  bool v18; // bl
  int v19; // eax
  int v20; // esi
  int v21; // ebx
  int v22; // ebx
  int v23; // eax
  int v24; // eax
  int v25; // eax
  int v26; // ebx
  int v28[68]; // [rsp+20h] [rbp-60h] BYREF
  char Str[1008]; // [rsp+130h] [rbp+B0h] BYREF
  int v30[1008]; // [rsp+520h] [rbp+4A0h] BYREF
  int v31[4]; // [rsp+14E0h] [rbp+1460h]
  int v32; // [rsp+14F0h] [rbp+1470h]
  int k; // [rsp+14F4h] [rbp+1474h]
  int j; // [rsp+14F8h] [rbp+1478h]
  int i; // [rsp+14FCh] [rbp+147Ch]

  _main(argc, argv, envp);
  memset(v30, 0, 0xFA0ui64);
  v30[1000] = 0;
  memset(v28, 0, 0x100ui64);
  v28[64] = 0;
  for ( i = 0; i <= 64; ++i )
    v28[i] = i + 1;
  v31[0] = 2;
  v31[1] = 3;
  v31[2] = 4;
  v31[3] = 5;
  v30[1004] = 2;
  v30[1005] = 3;
  v30[1006] = 4;
  v30[1007] = 5;
  puts("WHERE IS MY KEY!?");
  scanf("%32s", Str);
  v32 = strlen(Str);
  v3 = F0X1(v28[j], v28[j]);
  for ( j = v3 / v28[j]; j <= v32; ++j )
  {
    v4 = (v28[j] + v28[j + 1]) * (v28[j] + v28[j + 1]);
    if ( v4 >= (int)(F0X5(2, 2) * v28[j] * v28[j + 1]) )
    {
      v5 = ~Str[(int)F0X4(j, 1)];
      v6 = F0X4(j, 1);
      v30[j] = ~(v5 + v31[v6 % (int)F0X5(2, 2)]);
    }
    v7 = F0X1(v28[j], v28[j + 1]);
    if ( v7 > (int)F0X1(v28[j + 1], ~(~v28[j + 1] + v28[j])) )
    {
      v8 = v30[j];
      v9 = F0X4(j, 1);
      v30[j] = ~(~v8 + v28[v9 % (int)F0X5(2, 2)]) * v8;
    }
    v10 = v28[j + 1];
    v11 = F0X5(2, 1) * v10;
    v12 = v28[j];
    v13 = F0X5(2, 1);
    v14 = F0X1(v12 * v13, v11);
    v15 = F0X5(2, 1);
    if ( v14 == v15 * (unsigned int)F0X1(v28[j], v28[j + 1]) )
    {
      v16 = F0X4(j, 1);
      v30[j] ^= v31[v16 % (int)F0X5(2, 2)];
    }
    v17 = F0X5(V0X3, v28[j]);
    v18 = v17 < v28[j] + 1;
    v19 = F0X5(2, 4);
    if ( (unsigned __int8)F0X3(v19 >= j, v18) )
    {
      v20 = ~Str[(int)F0X4(j, 1)];
      v21 = F0X4(j, 1);
      v30[j] ^= ~(v20 + v31[v21 % (int)F0X5(2, 2)]);
    }
    v22 = F0X5(2, 3);
    v23 = F0X1(v28[j], v28[j]);
    v30[j] *= v22 + (unsigned int)F0X5(2, v23 / v28[j]);
  }
  v24 = F0X5(2, 4);
  if ( (unsigned int)F0X4(v24, 1) != v32 )
    goto LABEL_23;
  v25 = F0X1(v28[k], v28[k]);
  for ( k = v25 / v28[k]; k <= v32; ++k )
  {
    v26 = v30[k];
    if ( v26 == (int)F0X4(A0X6[k], 1) / 10 )
      ++V0X2;
  }
  if ( V0X2 == v32 )
    puts("\nPASS");
  else
LABEL_23:
    puts("\nDENIED");
  return 0;
}

首先查看 F0X1:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

__int64 __fastcall F0X1(unsigned int a1, int a2)
{
  __int64 result; // rax

  if ( a2 )
    result = F0X1(a2, (int)a1 % a2);
  else
    result = a1;
  return result;
}

这个递归函数容易发现是在求 a1 和 a2 的 gcd.

然后是 F0X5:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

__int64 __fastcall F0X5(int a1, int a2)
{
  unsigned int v4; // [rsp+Ch] [rbp-4h]

  v4 = 1;
  while ( a2 )
  {
    if ( (a2 & 1) != 0 )
      v4 *= a1;
    a1 *= a1;
    a2 >>= 1;
  }
  return v4;
}

这个也比较容易看出来, 就是在求 a1 的 a2 次方.

接着是 F0X4:

1
2
3
4

__int64 __fastcall F0X4(int a1, int a2)
{
  return (unsigned int)~(~a1 + a2);
}

对于两个 int 而言, 这个结构等价于 a1 - a2.

继续看 F0X3 和 F0X2:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

__int64 __fastcall F0X3(bool a1, bool a2)
{
  char v2; // bl
  char v3; // al

  v2 = F0X2(a2, a2);
  v3 = F0X2(a1, a1);
  return F0X2(v3, v2);
}

_BOOL8 __fastcall F0X2(char a1, char a2)
{
  return a1 == a2 && a1 != 1;
}

这个需要稍微推导一下, 可以看出等价于 a1 & a2

对于函数的功能, 可以考虑复制下来, 然后测试一下, 再结合推导, 就能比较容易的判断出函数的功能了.

于是进行重命名:

https://i.loli.net/2021/04/21/lneU2O8a6YhrpVC.png

  • 第一处:

    1
2

    v4 = (v28[j] + v28[j + 1]) * (v28[j] + v28[j + 1]);
if ( v4 >= (int)(pow(2, 2) * v28[j] * v28[j + 1]) )

    抽象出来即:

    $$ (x + y) ^ 2 \ge 4xy $$

    这是永真的, 也就是下面的代码块永远会被执行.

  • 第二处:

    1
2

    v7 = gcd(v28[j], v28[j + 1]);
if ( v7 > (int)gcd(v28[j + 1], ~(~v28[j + 1] + v28[j])) )

    等价于:

    $$ gcd(x, y) > gcd(y, x-y) $$

    左右两边显然是一样的, 所以下面的代码块不可能执行.

  • 第三处:

    1
2
3
4
5
6
7

    v10 = v28[j + 1];
v11 = pow(2, 1) * v10;
v12 = v28[j];
v13 = pow(2, 1);
v14 = gcd(v12 * v13, v11);
v15 = pow(2, 1);
if ( v14 == v15 * (unsigned int)gcd(v28[j], v28[j + 1]) )

    等价于:

    $$ gcd(2x, 2y) = 2gcd(x, y) $$

    这也是永真的, 故下面的代码块一定执行.

  • 第四处:

    1
2
3
4
5
6

    v17 = pow(V0X3, v28[j]);
v18 = v17 < v28[j] + 1;
v19 = pow(2, 4);
if ( (unsigned __int8)AND(v19 >= j, v18) )
//其中V0X3 == 3
//这里需要看看后面关于整个key长度的判断，这里就不说明了

    key 长度是 15 故 v19 >= j 必定成立

    于是只需判断:

    $$ f(x)=3^x - x - 1 <0 $$

    求导或者直接画图都能判断出该条件为假, 则下面的代码块不会执行.

  • 综上只有三处代码有效:

    https://i.loli.net/2021/04/21/i19yFkjOEmha56R.png

最终是这样的效果.

1
2
3
4
5
6
7
8

enc = [780, 780, 850, 590, 800, 640, 1150, 460, 980, 960, 1170, 530, 970, 1080, 1250]
vec = [2, 3, 4, 5]

for i in range(len(enc)):
    enc[i] = enc[i] // 10;
    enc[i] ^= vec[i%4]
    enc[i] += vec[i%4]
    print(chr(enc[i]), end="")

相关内容

「MiniLCTF2022」Rev | WhatAssembly & Lemon Official Writeup

「HITCONCTF2021」Rev复现

「DefcampCTF2022」Rev 部分题解

「RealWorldCTF2022」Rev | Trust_or_Not 基于 OPTEE 的安全存储分析

「CGCTF」部分练习记录

更新于 2021-04-21
阅读原始文档
 Rev
返回 | 主页