警告
本文最后更新于 2021-07-14,文中内容可能已过时。
在看雪论坛上偶然看到一个关于图片的逆向过程, 遂前往复现, 学到不少东西, 尤其是关于PE文件结构、手动脱壳、手写汇编脱壳以及 OD 的使用等等, 解决了很多以前的困惑, 就记录下来.
首先把图片拖进 010Editor, 发现正常的 png 图片结尾后, 还附带有大段的数据:
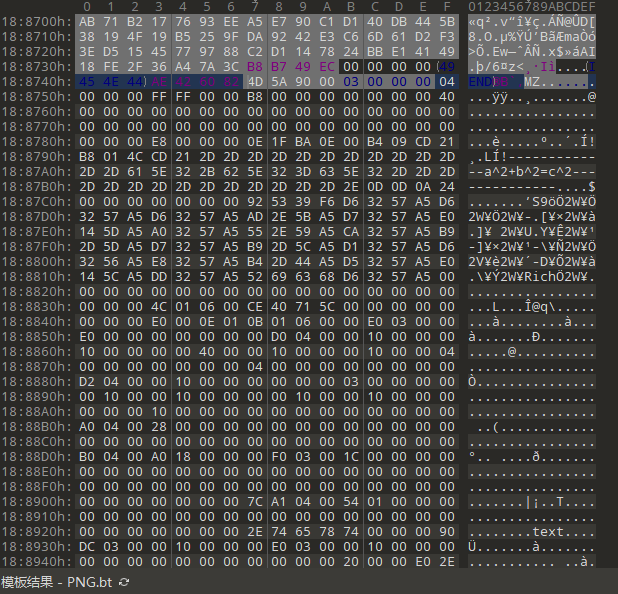
发现 DOS 头的 magic 字段, 即 MZ 之后, 猜测是在图片结尾附加一段 PE 文件, 于是将整个后半部分 dump 下来, 存在 bingo.exe 中, 但是这个是没法运行的.

根据 PE 文件结构, 我们主要关注 DOS 头的两个部分, 首先是 magic 字段, 即 MZ 字段, 还有一个就是 003Ch 的部分, 这一个 LONG 型数据指向了 NT 头的起始位置. 这个例子中 NT 头位置在 00E8h 的位置. 我们找到那个位置, 发现 PE 签名不见了, 我们手动补上后, 发现可以运行了, 但是只有一个 windows 控制台的子系统界面, 里面是没有内容的:
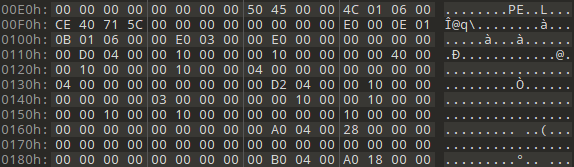
我们继续找 NT 头里面的 PE 可选文件头, 可以获取一些信息:
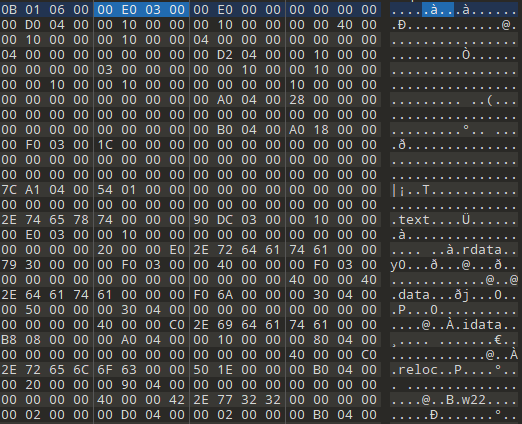
- 010Bh 表明是一个 32 位 PE 程序, 这个在 PE 文件头的 014Ch 处也能发觉
- 代码段长度为 3E000h, 已初始化数据段长度为 E00h, 未初始化数据段长度为 0, 程序入口RVA为 4D000h, 代码段 RVA 和数据段 RVA 都是 1000h
使用 OD 载入程序, 发现明显的加壳特征
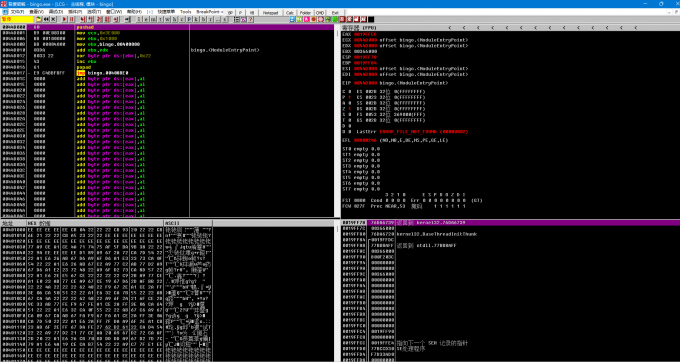
并且我们可以发现: 代码段的 RVA 和代码段的长度都出现了, 并且还有一个异或操作, 大胆猜测是一个 SMC 的过程.
但是他有一个地方写的有点问题, 就是他把 RVA 和代码段长都 mov 到了 ebx 里, 后面又加上了 edx, 这显然是不对的, 于是我们把修改和解壳的代码一并写入, 注意这里由于 AdvancedOlly 插件和 StrongOD 插件有冲突, 我们没法一次性复制到可执行文件, 我们只能先改一处的代码, 保存, 再改再保存, 除非你改的位置是连续的.
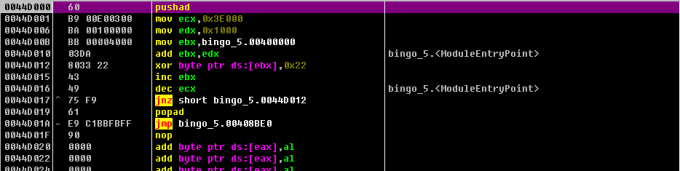
然后看到 pushad, 则利用ESP定律手动脱一下壳就成了, 不要忘记改一下 OEP.
拖进 IDA, main 函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| int __cdecl main_0(int argc, const char **argv, const char **envp)
{
char *Str1; // [esp+4Ch] [ebp-24h]
char input[32]; // [esp+50h] [ebp-20h] BYREF
memset(input, 0, 0x1Eu);
printf("毕达哥拉斯到底说了什么, 我很好奇!!\n:");
scanf("%s", input);
Str1 = (char *)proc_input(input, 52);
if ( !strcmp(Str1, Str2) )
printf("Right!!\n");
else
printf("False!!\n");
system("pause");
return 0;
}
|
拐进 proc_input 函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| // Str = input
// con = 52
char *__cdecl sub_401030(char *Str, int con)
{
int v3; // [esp+5Ch] [ebp-28h]
int v4; // [esp+6Ch] [ebp-18h]
signed int i; // [esp+70h] [ebp-14h]
char *new_space; // [esp+74h] [ebp-10h]
signed int Str_len; // [esp+78h] [ebp-Ch]
Str_len = strlen(Str);
new_space = (char *)operator new(Str_len + 1);
memset(new_space, 0, Str_len + 1);
for ( i = 0; i < Str_len; ++i )
{
v4 = (__int64)pow((double)con, 2.0);
v3 = (__int64)pow((double)Str[i], 2.0) - v4;
--con;
new_space[i] = (__int64)(sqrt((double)v3) + 0.5); // 这里 + 0.5 是为了保证进一位
_strrev(new_space);
}
return new_space;
}
|
稍微看看 _strrev, 效果是把整个字符串反过来:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| char *__cdecl _strrev(char *Str)
{
char *v1; // esi
unsigned int v2; // kr04_4
char *i; // edi
char tmp; // ah
v1 = Str;
v2 = strlen(Str) + 1;
if ( ~v2 != -2 )
{
for ( i = &Str[v2 - 2]; v1 < i; --i )
{
tmp = *v1;
*v1 = *i;
*i = tmp;
++v1;
}
}
return Str;
}
|
脚本比较巧妙, 因为这个加密算法就是比较巧妙的, flag 长度必须是奇数
我们可以很容易证明一个性质: 就是 i 为偶数时 p[i] 一定在 p[len - 1 - i] 的地方;i 为奇数时 p[i] 一定在原来的地方.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| #include <stdio.h>
#include <string.h>
#include <math.h>
char* _strrev(char *Str) { // 把整个字符串反过来
char *v1;
unsigned int v2 = strlen(Str) + 1;
char tmp;
v1 = Str;
if ( ~v2 != -2 ) { // <=> if strlen(str) != 0
for (char* i = &Str[v2 - 2]; v1 < i; --i ) { // i向前遍历Str, 直到v1和i相遇
tmp = *v1;
*v1 = *i;
*i = tmp;
++v1; // v1向后遍历Str
}
}
return Str;
}
int main() {
char enc_flag[] = "zaciWjV!Xm[_XSqeThmegndq";
int flag_len = strlen(enc_flag);
char flag[25] = {0};
memset(flag, 0, flag_len + 1);
int c = 52 - flag_len + 1;
for (int i =0; i < flag_len; i++) {
char tmp = enc_flag[0];
_strrev(enc_flag);
enc_flag[flag_len - 1 - i] = '\0';
int y = pow(c, 2.0);
int z = pow((double)tmp, 2.0) + y;
int zz = int((double)sqrt(z) + 0.5);
flag[flag_len - 1 - i] = zz;
c ++;
}
printf("The reverse string of enc_flag is: %s\n", flag);
return 0;
}
|





